マイクラで論理回路
- Koma(in motion)
- 2021年10月19日
みんなは、論理演算とか得意だろうか。俺は苦手である。
ただいま勉強中の基本情報技術者試験においても、論理演算とか論理回路に関する問題が出題されることがある。演算なんだから、時間をかければ解ける問題なんだが、根本的に「頭使いたくない病」患者なので、もっと用語丸暗記で対応できる問題が好きだ・・・。
いや、そんなこと言って俺ももう立派なオバサー(over thirty)だしな、記憶力に関してももう心許ないかもしれない・・・。
今回は、嫌いな論理回路を楽しく勉強しようということで、PS4のMinecraftで論理回路を設計してみようという企画。
とりあえず、マイクラをよく知らない人に説明しておくと、
マイクラには電力の概念があって、電源となるオブジェクトが存在する。例えばレバー。以前の記事でも、波動エンジンおよび波動砲のスイッチとして使用していたが、下の図のようにレバーとランプをレッドストーンという粉で繋いでやって・・・

レバーをONにするとランプが点灯する。

まぁ、これだけだとA = Aみたいなもんで、論理回路なんてできるの?って感じだが、マイクラの世界は異常に奥が深いので、もっと複雑なアルゴリズムを実現可能にするようなオブジェクトがいろいろ存在する。その中の一つが、レッドストーントーチ。

レッドストーントーチは、それ自体が電源としても使えるんだけど、「設置されているブロックに電力が供給されている時、OFFになる」という特性がある。
下の図のように回路を繋ぐと、レバーをOFFにしている間はランプは点灯する。

レバーをOFにするとランプは消える。

つまり、このレッドストーントーチ自体が「NOT回路」の役割をしているということ!

Aが真ならQは偽、Aが偽ならQは真。そういうゲート。今回は主にこれを利用して、代表的な論理回路を設計していく!
OR回路(論理和)
まずは簡単なやつから。AかBの少なくとも一方が真なら結果は真になればいい。
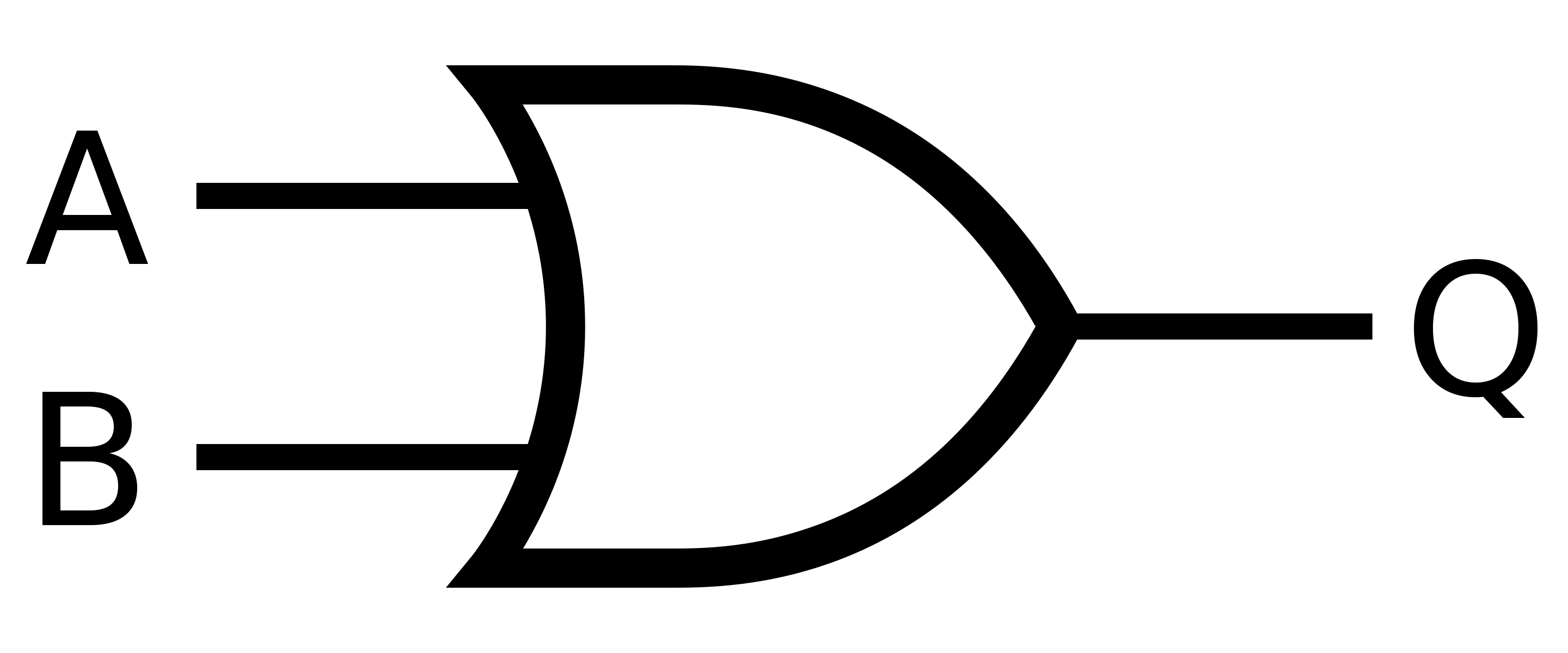
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
これは何の小細工もなくこんな感じ。

少なくともどちらか片方のレバーがONになっていればランプがつく。楽勝だでな。
AND回路(論理積)
次、Aが真、かつBが真の時だけ真になる論理積。わかりやすいけど、これをマイクラで設計しようとすると急にこんがらがる。

| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
試行錯誤した結果から伝えると、こう!

トーチによるNOTゲートを3つ使ってる。どういうことかというと、まず、ANDの論理式って、Q = A・Bで表せるんだけど、この式を変換しようとすると、

こんな感じにできないだろうか。AかつBの補集合の補集合、つまり「AかつBでないもの、の否定」。は?って感じだけど、これを中学で習ったような気もする「ド・モルガンの法則」に当てはめると、さらに次のように変換できる。

Aの補集合とBの補集合の論理和、の補集合。「Aでない、もしくはBでないもの、の否定」。頭こんがらがってきたが、これならトーチのNOTゲートで表現できる。さっきの画像で示すなら

こういうことじゃろがい!
AND回路なので、どちらか一方のレバーでもOFFだとランプは点灯しない。

もちろん両方OFFでも灯かない。

NAND回路(否定論理積)
次、NAND回路。Aが真、かつBが真の時のみ結果が偽になる。

| A | B | Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
ややこしそうに見えて、実はAND回路よりよっぽど簡単なんだよな。NANDの論理式は

こう。この変換はド・モルガンの法則まさにそのもので、

こう。マイクラで再現すると

こうでっしゃろがい!ぶたさんも興味深々やでぇ。
レバーを両方ともONにしてしまうとランプが消灯する。

ANDより先にこっち作るべきだったかもしれない。
NOR回路(否定論理和)
次、NOR回路。Aが真、もしくはBが真だと結果は偽になる。

| A | B | Q |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
これも簡単。NORの論理式は

こうなので、そのままマイクラで再現すると

こうやねん!
どちらかのレバーをONにしてしまうと、ランプは消灯する。

XOR回路(排他的論理和)
最後に、XOR回路。Aが真かつBが偽、もしくはAが偽かつBが真、の時だけ結果が真。これがなかなかややこしい。

| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
まず、「Aが真かつBが偽、もしくはAが偽かつBが真」なんだから、論理式としては

こうなるんだけど、これを

こう変換して見た。
とりあえず、左辺の

から作るか・・・

こうかな。A(左)のレバーがON、かつBのレバーがOFFの時だけランプが点灯する回路。
右辺の方はこれのまるっきり逆なので

こう。
あとは、この左辺と右辺をOR回路として繋いでやればいいので・・・

こう!!
両方のレバーがON、あるいは両方OFFだとランプは点灯しない。

一応、理屈としてはあってるんだけど・・・デカすぎるし不恰好だな。実はもっとコンパクトにまとめる方法があって、それがこれ。

細かい解説は面倒なので省くけど、挙動としてはさっきのと全く同じものになる。
とまぁ、これで主要な論理回路については一通り設計できた。本当はこいつらを組み合わせて試験問題の解答を検証とかしようと思ったのだが、さすがにサラリーマンが平日にやることではないと気づいたので、またの機会にする。
